Graham's scan

Graham's scan solves the convex-hull problem by maintaining a stack S of candidate points. Each point of the input set Q is pushed once onto the stack, and the points that are not vertices of CH(Q) are eventually popped from the stack. When the algorithm terminates, stack S contains exactly the vertices of CH(Q), in counterclockwise order of their appearance on the boundary.

The procedure GRAHAM-SCAN takes as input a set Q of points, where |Q| ≥ 3. It calls the functions TOP(S), which returns the point on top of stack S without changing S, and NEXT-TO-TOP(S), which returns the point one entry below the top of stack S without changing S. As we shall prove in a moment, the stack S returned by GRAHAM-SCAN contains, from bottom to top, exactly the vertices of CH(Q) in counterclockwise order.

GRAHAM-SCAN(Q)
 1  let p0 be the point in Q with the minimum y-coordinate,
             or the leftmost such point in case of a tie
 2  let 〈p1, p2, ..., pm〉 be the remaining points in Q,
             sorted by polar angle in counterclockwise order around p0
             (if more than one point has the same angle, remove all but
             the one that is farthest from p0)
 3  PUSH(p0, S)
 4  PUSH(p1, S)
 5  PUSH(p2, S)
 6  for i ← 3 to m
 7       do while the angle formed by points NEXT-TO-TOP(S), TOP(S),
                     and pi makes a nonleft turn
 8              do POP(S)
 9          PUSH(pi, S)
10  return S

Figure 33.7 illustrates the progress of GRAHAM-SCAN. Line 1 chooses point p₀ as the point with the lowest y-coordinate, picking the leftmost such point in case of a tie. Since there is no point in Q that is below p₀ and any other points with the same y-coordinate are to its right, p₀ is a vertex of CH(Q). Line 2 sorts the remaining points of Q by polar angle relative to p₀, using the same method-comparing cross products-as in Exercise 33.1-3. If two or more points have the same polar angle relative to p₀, all but the farthest such point are convex combinations of p₀ and the farthest point, and so we remove them entirely from consideration. We let m denote the number of points other than p₀ that remain. The polar angle, measured in radians, of each point in Q relative to p₀ is in the half-open interval [0, π). Since the points are sorted according to polar angles, they are sorted in counterclockwise order relative to p₀. We designate this sorted sequence of points by 〈p₁, p₂, ..., p_m〉. Note that points p₁ and p_m are vertices of CH(Q) (see Exercise 33.3-1). Figure 33.7(a) shows the points of Figure 33.6 sequentially numbered in order of increasing polar angle relative to p₀.

 
Figure 33.7: The execution of GRAHAM-SCAN on the set Q of Figure 33.6. The current convex hull contained in stack S is shown in gray at each step. (a) The sequence 〈 p₁, p₂, ..., p₁₂〉 of points numbered in order of increasing polar angle relative to p₀, and the initial stack S containing p₀, p₁, and p₂. (b)-(k) Stack S after each iteration of the for loop of lines 6-9. Dashed lines show nonleft turns, which cause points to be popped from the stack. In part (h), for example, the right turn at angle ∠p₇p₈p₉ causes p₈ to be popped, and then the right turn at angle ∠p₆p₇p₉ causes p₇ to be popped. (l) The convex hull returned by the procedure, which matches that of Figure 33.6.

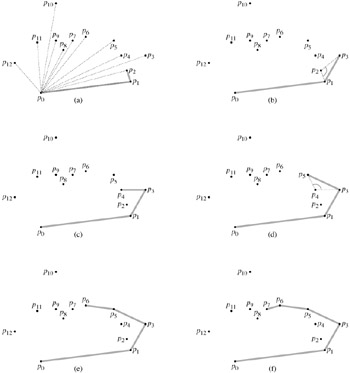
The remainder of the procedure uses the stack S. Lines 3-5 initialize the stack to contain, from bottom to top, the first three points p₀, p₁, and p₂. Figure 33.7(a) shows the initial stack S. The for loop of lines 6-9 iterates once for each point in the subsequence 〈p₃, p₄, ..., p_m〉. The intent is that after processing point p_i , stack S contains, from bottom to top, the vertices of CH({ p₀, p₁, ..., p_i}) in counterclockwise order. The while loop of lines 7-8 removes points from the stack if they are found not to be vertices of the convex hull. When we traverse the convex hull counterclockwise, we should make a left turn at each vertex. Thus, each time the while loop finds a vertex at which we make a nonleft turn, the vertex is popped from the stack. (By checking for a nonleft turn, rather than just a right turn, this test precludes the possibility of a straight angle at a vertex of the resulting convex hull. We want no straight angles, since no vertex of a convex polygon may be a convex combination of other vertices of the polygon.) After we pop all vertices that have nonleft turns when heading toward point p_i , we push p_i onto the stack. Figures 33.7(b)-(k) show the state of the stack S after each iteration of the for loop. Finally, GRAHAM-SCAN returns the stack S in line 10. Figure 33.7(l) shows the corresponding convex hull.

The following theorem formally proves the correctness of GRAHAM-SCAN.

Theorem 33.1: (Correctness of Graham's scan)

If GRAHAM-SCAN is run on a set Q of points, where |Q| ≥ 3, then at termination, the stack S consists of, from bottom to top, exactly the vertices of CH(Q) in counterclockwise order.

Proof After line 2, we have the sequence of points 〈p₁, p₂, ..., p_m〉. Let us define, for i = 2, 3, ..., m, the subset of points Q_i = {p₀, p₁, ..., p_i}. The points in Q - Q_m are those that were removed because they had the same polar angle relative to p₀ as some point in Q_m; these points are not in CH(Q), and so CH(Q_m) = CH(Q). Thus, it suffices to show that when GRAHAM-SCAN terminates, the stack S consists of the vertices of CH(Q_m) in counterclockwise order from bottom to top. Note that just as p₀, p₁, and p_m are vertices of CH(Q), the points p₀, p₁, and p_i are all vertices of CH(Q_i).

The proof uses the following loop invariant:

• At the start of each iteration of the for loop of lines 6-9, stack S consists of, from bottom to top, exactly the vertices of CH(Q_i-1) in counterclockwise order.

• Initialization: The invariant holds the first time we execute line 6, since at that time, stack S consists of exactly the vertices of Q₂ = Q_i-1, and this set of three vertices forms its own convex hull. Moreover, they appear in counterclockwise order from bottom to top.

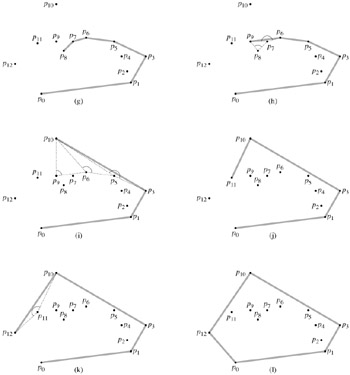
• Maintenance: Entering an iteration of the for loop, the top point on stack S is p_i-1, which was pushed at the end of the previous iteration (or before the first iteration, when i = 3). Let p_j be the top point on S after the while loop of lines 7-8 is executed but before line 9 pushes p_i, and let p_k be the point just below p_j on S. At the moment that p_j is the top point on S and we have not yet pushed p_i, stack S contains exactly the same points it contained after iteration j of the for loop. By the loop invariant, therefore, S contains exactly the vertices of CH(Q_j) at that moment, and they appear in counterclockwise order from bottom to top.

  Let us continue to focus on this moment just before p_i is pushed. Referring to Figure 33.8(a), because p_i's polar angle relative to p₀ is greater than p_j's polar angle, and because the angle ∠p_kp_jp_i makes a left turn (otherwise we would have popped p_j ), we see that since S contains exactly the vertices of CH(Q_j), once we push p_i , stack S will contain exactly the vertices of CH(Q_j ∪ {p_i}), still in counterclockwise order from bottom to top.

  
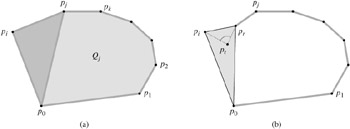
  Figure 33.8: The proof of correctness of GRAHAM-SCAN. (a) Because p_i's polar angle relative to p₀ is greater than p_j's polar angle, and because the angle ∠p_kp_j p_i makes a left turn, adding p_i to CH(Q_j) gives exactly the vertices of CH(Q_j ∪{p_i}). (b) If the angle ∠p_rp_tp_i makes a nonleft turn, then p_t is either in the interior of the triangle formed by p₀, p_r, and p_i or on a side of the triangle, and it cannot be a vertex of CH(Q_i).

  We now show that CH(Q_j ∪ {p_i}) is the same set of points as CH(Q_i). Consider any point p_t that was popped during iteration i of the for loop, and let p_r be the point just below p_t on stack S at the time p_t was popped (p_r might be p_j ). The angle ∠p_rp_tp_i makes a nonleft turn, and the polar angle of p_t relative to p₀ is greater than the polar angle of p_r. As Figure 33.8(b) shows, p_t must be either in the interior of the triangle formed by p₀, p_r, and p_i or on a side of this triangle (but it is not a vertex of the triangle). Clearly, since p_t is within a triangle formed by three other points of Q_i, it cannot be a vertex of CH(Q_i). Since p_t is not a vertex of CH(Q_i), we have that

  (33.1)

  Let P_i be the set of points that were popped during iteration i of the for loop. Since the equality (33.1) applies for all points in P_i, we can apply it repeatedly to show that CH(Q_i - P_i) = CH(Q_i). But Q_i - P_i = Q_j ∪ {p_i}, and so we conclude that CH(Q_j ∪ {p_i}) = CH(Q_i - P_i) = CH(Q_i).

  We have shown that once we push p_i , stack S contains exactly the vertices of CH(Q_i) in counterclockwise order from bottom to top. Incrementing i will then cause the loop invariant to hold for the next iteration.

• Termination: When the loop terminates, we have i = m + 1, and so the loop invariant implies that stack S consists of exactly the vertices of CH(Q_m), which is CH(Q), in counterclockwise order from bottom to top. This completes the proof.

We now show that the running time of GRAHAM-SCAN is O(n lg n), where n = |Q|. Line 1 takes Θ(n) time. Line 2 takes O(n lg n) time, using merge sort or heapsort to sort the polar angles and the cross-product method of Section 33.1 to compare angles. (Removing all but the farthest point with the same polar angle can be done in a total of O(n) time.) Lines 3-5 take O(1) time. Because m ≤ n - 1, the for loop of lines 6-9 is executed at most n - 3 times. Since PUSH takes O(1) time, each iteration takes O(1) time exclusive of the time spent in the while loop of lines 7-8, and thus overall the for loop takes O(n) time exclusive of the nested while loop.

We use aggregate analysis to show that the while loop takes O(n) time overall. For i = 0, 1, ..., m, each point p_i is pushed onto stack S exactly once. As in the analysis of the MULTIPOP procedure of Section 17.1, we observe that there is at most one POP operation for each PUSH operation. At least three points-p₀, p₁, and p_m-are never popped from the stack, so that in fact at most m - 2 POP operations are performed in total. Each iteration of the while loop performs one POP, and so there are at most m - 2 iterations of the while loop altogether. Since the test in line 7 takes O(1) time, each call of POP takes O(1) time, and since m ≤ n - 1, the total time taken by the while loop is O(n). Thus, the running time of GRAHAM-SCAN is O(n lg n).

Jarvis's march

Jarvis's march computes the convex hull of a set Q of points by a technique known as package wrapping (or gift wrapping). The algorithm runs in time O(nh), where h is the number of vertices of CH(Q). When h is o(lg n), Jarvis's march is asymptotically faster than Graham's scan.

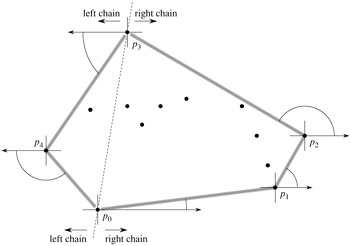
Intuitively, Jarvis's march simulates wrapping a taut piece of paper around the set Q. We start by taping the end of the paper to the lowest point in the set, that is, to the same point p₀ with which we start Graham's scan. This point is a vertex of the convex hull. We pull the paper to the right to make it taut, and then we pull it higher until it touches a point. This point must also be a vertex of the convex hull. Keeping the paper taut, we continue in this way around the set of vertices until we come back to our original point p₀.

More formally, Jarvis's march builds a sequence H = 〈p₀, p₁, ..., p_h-1〉 of the vertices of CH(Q). We start with p₀. As Figure 33.9 shows, the next convex hull vertex p₁ has the smallest polar angle with respect to p₀. (In case of ties, we choose the point farthest from p₀.) Similarly, p₂ has the smallest polar angle with respect to p₁, and so on. When we reach the highest vertex, say p_k (breaking ties by choosing the farthest such vertex), we have constructed, as Figure 33.9 shows, the right chain of CH(Q). To construct the left chain, we start at p_k and choose p_k+1 as the point with the smallest polar angle with respect to p_k, but from the negative x-axis. We continue on, forming the left chain by taking polar angles from the negative x-axis, until we come back to our original vertex p₀.

Figure 33.9: The operation of Jarvis's march. The first vertex chosen is the lowest point p₀. The next vertex, p₁, has the smallest polar angle of any point with respect to p₀. Then, p₂ has the smallest polar angle with respect to p₁. The right chain goes as high as the highest point p₃. Then, the left chain is constructed by finding smallest polar angles with respect to the negative x-axis.

We could implement Jarvis's march in one conceptual sweep around the convex hull, that is, without separately constructing the right and left chains. Such implementations typically keep track of the angle of the last convex-hull side chosen and require the sequence of angles of hull sides to be strictly increasing (in the range of 0 to 2π radians). The advantage of constructing separate chains is that we need not explicitly compute angles; the techniques of Section 33.1 suffice to compare angles.

If implemented properly, Jarvis's march has a running time of O(nh). For each of the h vertices of CH(Q), we find the vertex with the minimum polar angle. Each comparison between polar angles takes O(1) time, using the techniques of Section 33.1. As Section 9.1 shows, we can compute the minimum of n values in O(n) time if each comparison takes O(1) time. Thus, Jarvis's march takes O(nh) time.

Exercises 33.3-1

Prove that in the procedure GRAHAM-SCAN, points p₁ and p_m must be vertices of CH(Q).

Exercise 33.3-2

Consider a model of computation that supports addition, comparison, and multiplication and for which there is a lower bound of Ω(n lg n) to sort n numbers. Prove that Ω(n lg n) is a lower bound for computing, in order, the vertices of the convex hull of a set of n points in such a model.

Exercise 33.3-3

Given a set of points Q, prove that the pair of points farthest from each other must be vertices of CH(Q).

Exercise 33.3-4

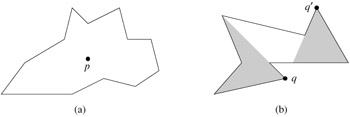
For a given polygon P and a point q on its boundary, the shadow of q is the set of points r such that the segment is entirely on the boundary or in the interior of P.

A polygon P is star-shaped if there exists a point p in the interior of P that is in the shadow of every point on the boundary of P. The set of all such points p is called the kernel of P. (See Figure 33.10.) Given an n-vertex, star-shaped polygon P specified by its vertices in counterclockwise order, show how to compute CH(P) in O(n) time.

Figure 33.10: The definition of a star-shaped polygon, for use in Exercise 33.3-4. (a) A star-shaped polygon. The segment from point p to any point q on the boundary intersects the boundary only at q. (b) A non-star-shaped polygon. The shaded region on the left is the shadow of q, and the shaded region on the right is the shadow of q′. Since these regions are disjoint, the kernel is empty.

Exercise 33.3-5

In the on-line convex-hull problem, we are given the set Q of n points one point at a time. After receiving each point, we are to compute the convex hull of the points seen so far. Obviously, we could run Graham's scan once for each point, with a total running time of O(n² lg n). Show how to solve the on-line convex-hull problem in a total of O(n²) time.

Exercise 33.3-6: ⋆

Show how to implement the incremental method for computing the convex hull of n points so that it runs in O(n lg n) time.