Stack operations

In our first example of aggregate analysis, we analyze stacks that have been augmented with a new operation. Section 10.1 presented the two fundamental stack operations, each of which takes O(1) time:

PUSH(S, x) pushes object x onto stack S.

POP(S) pops the top of stack S and returns the popped object.

Since each of these operations runs in O(1) time, let us consider the cost of each to be 1. The total cost of a sequence of n PUSH and POP operations is therefore n, and the actual running time for n operations is therefore Θ(n).

Now we add the stack operation MULTIPOP(S,k), which removes the k top objects of stack S, or pops the entire stack if it contains fewer than k objects. In the following pseudocode, the operation STACK-EMPTY returns TRUE if there are no objects currently on the stack, and FALSE otherwise.

MULTIPOP(S, k)
1  while not STACK-EMPTY(S) and k ≠ 0
2     do POP(S)
3        k → k - 1

Figure 17.1 shows an example of MULTIPOP.

Figure 17.1: The action of MULTIPOP on a stack S, shown initially in (a). The top 4 objects are popped by MULTIPOP(S, 4), whose result is shown in (b). The next operation is MULTIPOP(S, 7), which empties the stack-shown in (c)-since there were fewer than 7 objects remaining.

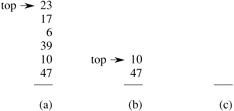
What is the running time of MULTIPOP(S, k) on a stack of s objects? The actual running time is linear in the number of POP operations actually executed, and thus it suffices to analyze MULTIPOP in terms of the abstract costs of 1 each for PUSH and POP. The number of iterations of the while loop is the number min(s, k)of objects popped off the stack. For each iteration of the loop, one call is made to POP in line 2. Thus, the total cost of MULTIPOP is min(s,k), and the actual running time is a linear function of this cost.

Let us analyze a sequence of n PUSH, POP, and MULTIPOP operations on an initially empty stack. The worst-case cost of a MULTIPOP operation in the sequence is O(n), since the stack size is at most n. The worst-case time of any stack operation is therefore O(n), and hence a sequence of n operations costs O(n²), since we may have O(n) MULTIPOP operations costing O(n) each. Although this analysis is correct, the O(n²) result, obtained by considering the worst-case cost of each operation individually, is not tight.

Using aggregate analysis, we can obtain a better upper bound that considers the entire sequence of n operations. In fact, although a single MULTIPOP operation can be expensive, any sequence of n PUSH, POP, and MULTIPOP operations on an initially empty stack can cost at most O(n). Why? Each object can be popped at most once for each time it is pushed. Therefore, the number of times that POP can be called on a nonempty stack, including calls within MULTIPOP, is at most the number of PUSH operations, which is at most n. For any value of n, any sequence of n PUSH, POP, and MULTIPOP operations takes a total of O(n) time. The average cost of an operation is O(n)/n = O(1). In aggregate analysis, we assign the amortized cost of each operation to be the average cost. In this example, therefore, all three stack operations have an amortized cost of O(1).

We emphasize again that although we have just shown that the average cost, and hence running time, of a stack operation is O(1), no probabilistic reasoning was involved. We actually showed a worst-case bound of O(n) on a sequence of n operations. Dividing this total cost by n yielded the average cost per operation, or the amortized cost.

Incrementing a binary counter

As another example of aggregate analysis, consider the problem of implementing a k-bit binary counter that counts upward from 0. We use an array A[0 ‥ k -1] of bits, where length[A] = k, as the counter. A binary number x that is stored in the counter has its lowest-order bit in A[0] and its highest-order bit in A[k - 1], so that . Initially, x = 0, and thus A[i] = 0 for i = 0, 1, ..., k - 1. To add 1 (modulo 2^k) to the value in the counter, we use the following procedure.

INCREMENT(A)
1  i ← 0
2  while i < length[A] and A[i] = 1
3     do A[i] ← 0
4           i ← i + 1
5  if i < length[A]
6     then A[i] ← 1

Figure 17.2 shows what happens to a binary counter as it is incremented 16 times, starting with the initial value 0 and ending with the value 16. At the start of each iteration of the while loop in lines 2-4, we wish to add a 1 into position i. If A[i] = 1, then adding 1 flips the bit to 0 in position i and yields a carry of 1, to be added into position i + 1 on the next iteration of the loop. Otherwise, the loop ends, and then, if i < k, we know that A[i] = 0, so that adding a 1 into position i, flipping the 0 to a 1, is taken care of in line 6. The cost of each INCREMENT operation is linear in the number of bits flipped.

Figure 17.2: An 8-bit binary counter as its value goes from 0 to 16 by a sequence of 16 INCREMENT operations. Bits that flip to achieve the next value are shaded. The running cost for flipping bits is shown at the right. Notice that the total cost is never more than twice the total number of INCREMENT operations.

As with the stack example, a cursory analysis yields a bound that is correct but not tight. A single execution of INCREMENT takes time Θ(k) in the worst case, in which array A contains all ′s. Thus, a sequence of n INCREMENT operations on an initially zero counter takes time O(nk) in the worst case.

We can tighten our analysis to yield a worst-case cost of O(n) for a sequence of n INCREMENT's by observing that not all bits flip each time INCREMENT is called. As Figure 17.2 shows, A[0] does flip each time INCREMENT is called. The next-highest-order bit, A[1], flips only every other time: a sequence of n INCREMENT operations on an initially zero counter causes A[1] to flip ⌈n/2⌉ times. Similarly, bit A[2] flips only every fourth time, or ⌈n/4⌉ times in a sequence of n INCREMENT's. In general, for i = 0, 1, ..., ⌈lg n⌉, bit A[i] flips ⌈n/2ⁱ⌉ times in a sequence of n INCREMENT operations on an initially zero counter. For i > ⌈lg n⌉, bit A[i] never flips at all. The total number of flips in the sequence is thus

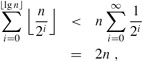
by equation (A.6). The worst-case time for a sequence of n INCREMENT operations on an initially zero counter is therefore O(n). The average cost of each operation, and therefore the amortized cost per operation, is O(n)/n = O(1).

Exercises 17.1-1

If the set of stack operations included a MULTIPUSH operation, which pushes k items onto the stack, would the O(1) bound on the amortized cost of stack operations continue to hold?

Exercises 17.1-2

Show that if a DECREMENT operation were included in the k-bit counter example, n operations could cost as much as Θ(nk) time.

Exercises 17.1-3

A sequence of n operations is performed on a data structure. The ith operation costs i if i is an exact power of 2, and 1 otherwise. Use aggregate analysis to determine the amortized cost per operation.