| < Day Day Up > |
This section contains a proof of the master theorem (Theorem 4.1). The proof need not be understood in order to apply the theorem.
The proof is in two parts. The first part analyzes the "master" recurrence (4.5), under the simplifying assumption that T(n) is defined only on exact powers of b > 1, that is, for n = 1, b, b2, ..‥ This part gives all the intuition needed to understand why the master theorem is true. The second part shows how the analysis can be extended to all positive integers n and is merely mathematical technique applied to the problem of handling floors and ceilings.
In this section, we shall sometimes abuse our asymptotic notation slightly by using it to describe the behavior of functions that are defined only over exact powers of b. Recall that the definitions of asymptotic notations require that bounds be proved for all sufficiently large numbers, not just those that are powers of b. Since we could make new asymptotic notations that apply to the set {bi : i = 0, 1,...}, instead of the nonnegative integers, this abuse is minor.
Nevertheless, we must always be on guard when we are using asymptotic notation over a limited domain so that we do not draw improper conclusions. For example, proving that T (n) = O(n) when n is an exact power of 2 does not guarantee that T (n) = O(n). The function T (n) could be defined as
in which case the best upper bound that can be proved is T (n) = O(n2). Because of this sort of drastic consequence, we shall never use asymptotic notation over a limited domain without making it absolutely clear from the context that we are doing so.
The first part of the proof of the master theorem analyzes the recurrence (4.5)
T (n) = aT (n/b) + f (n) ,
for the master method, under the assumption that n is an exact power of b > 1, where b need not be an integer. The analysis is broken into three lemmas. The first reduces the problem of solving the master recurrence to the problem of evaluating an expression that contains a summation. The second determines bounds on this summation. The third lemma puts the first two together to prove a version of the master theorem for the case in which n is an exact power of b.
Let a ≥ 1 and b > 1 be constants, and let f (n) be a nonnegative function defined on exact powers of b. Define T (n) on exact powers of b by the recurrence
where i is a positive integer. Then
Proof We use the recursion tree in Figure 4.3. The root of the tree has cost f (n), and it has a children, each with cost f (n/b). (It is convenient to think of a as being an integer, especially when visualizing the recursion tree, but the mathematics does not require it.) Each of these children has a children with cost f (n/b2), and thus there are a2 nodes that are distance 2 from the root. In general, there are aj nodes that are distance j from the root, and each has cost f (n/bj). The cost of each leaf is T (1) = Θ(1), and each leaf is at depth logb n, since ![]() . There are
. There are ![]() leaves in the tree.
leaves in the tree.
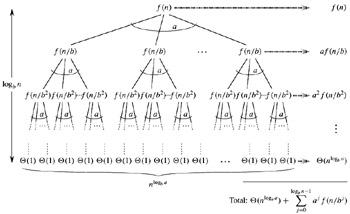
We can obtain equation (4.6) by summing the costs of each level of the tree, as shown in the figure. The cost for a level j of internal nodes is aj f(n/bj), and so the total of all internal node levels is
In the underlying divide-and-conquer algorithm, this sum represents the costs of dividing problems into subproblems and then recombining the subproblems. The cost of all the leaves, which is the cost of doing all ![]() subproblems of size 1, is
subproblems of size 1, is ![]() .
.
In terms of the recursion tree, the three cases of the master theorem correspond to cases in which the total cost of the tree is (1) dominated by the costs in the leaves, (2) evenly distributed across the levels of the tree, or (3) dominated by the cost of the root.
The summation in equation (4.6) describes the cost of the dividing and combining steps in the underlying divide-and-conquer algorithm. The next lemma provides asymptotic bounds on the summation's growth.
Let a ≥ 1 and b > 1 be constants, and let f(n) be a nonnegative function defined on exact powers of b. A function g(n) defined over exact powers of b by
can then be bounded asymptotically for exact powers of b as follows.
If ![]() for some constant ∈ > 0, then
for some constant ∈ > 0, then ![]() .
.
If ![]() , then
, then ![]() .
.
If af (n/b) ≤ cf(n) for some constant c < 1 and for all n ≥ b, then g(n) = Θ(f(n)).
Proof For case 1, we have ![]() , which implies that
, which implies that ![]()
![]() . Substituting into equation (4.7) yields
. Substituting into equation (4.7) yields
We bound the summation within the O-notation by factoring out terms and simplifying, which leaves an increasing geometric series:
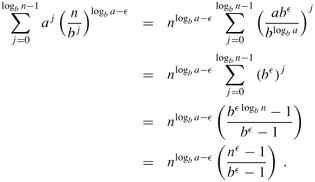
Since b and ∈ are constants, we can rewrite the last expression as ![]()
![]() . Substituting this expression for the summation in equation (4.8) yields
. Substituting this expression for the summation in equation (4.8) yields
and case 1 is proved.
Under the assumption that ![]() for case 2, we have that
for case 2, we have that ![]()
![]() . Substituting into equation (4.7) yields
. Substituting into equation (4.7) yields
We bound the summation within the Θ as in case 1, but this time we do not obtain a geometric series. Instead, we discover that every term of the summation is the same:
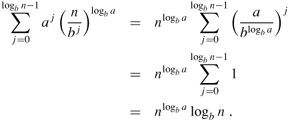
Substituting this expression for the summation in equation (4.9) yields
|
g(n) |
= |
( |
|
= |
( |
Case 3 is proved similarly. Since f(n) appears in the definition (4.7) of g(n) and all terms of g(n) are nonnegative, we can conclude that g(n) = Ω(f(n)) for exact powers of b. Under our assumption that af(n/b) ≤ cf(n) for some constant c < 1 and all n ≥ b, we have f(n/b) ≤ (c/a)f(n). Iterating j times, we have f(n/bj) ≤ (c/a)j f(n) or, equivalently, aj f(n/bj) ≤ cj f(n). Substituting into equation (4.7) and simplifying yields a geometric series, but unlike the series in case 1, this one has decreasing terms:
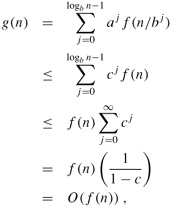
since c is constant. Thus, we can conclude that g(n) = Θ(f(n)) for exact powers of b. Case 3 is proved, which completes the proof of the lemma.
We can now prove a version of the master theorem for the case in which n is an exact power of b.
Let a ≥ 1 and b > 1 be constants, and let f(n) be a nonnegative function defined on exact powers of b. Define T(n) on exact powers of b by the recurrence
where i is a positive integer. Then T(n) can be bounded asymptotically for exact powers of b as follows.
If ![]() for some constant ∈ > 0, then
for some constant ∈ > 0, then ![]() .
.
If ![]() , then
, then ![]() .
.
If ![]() for some constant ∈ > 0, and if af (n/b) ≤ cf(n) for some constant c < 1 and all sufficiently large n, then T(n) = Θ(f(n)).
for some constant ∈ > 0, and if af (n/b) ≤ cf(n) for some constant c < 1 and all sufficiently large n, then T(n) = Θ(f(n)).
Proof We use the bounds in Lemma 4.3 to evaluate the summation (4.6) from Lemma 4.2. For case 1, we have
|
T(n) |
= |
|
|
= |
|
and for case 2,
|
T(n) |
= |
|
|
= |
|
For case 3,
|
T(n) |
= |
|
|
= |
Θ(f(n)), |
because ![]() .
.
To complete the proof of the master theorem, we must now extend our analysis to the situation in which floors and ceilings are used in the master recurrence, so that the recurrence is defined for all integers, not just exact powers of b. Obtaining a lower bound on
and an upper bound on
is routine, since the bound ⌈n/b⌉ ≥ n/b can be pushed through in the first case to yield the desired result, and the bound ⌊n/b⌋ ≤ n/b can be pushed through in the second case. Lower bounding the recurrence (4.11) requires much the same technique as upper bounding the recurrence (4.10), so we shall present only this latter bound.
We modify the recursion tree of Figure 4.3 to produce the recursion tree in Figure 4.4. As we go down in the recursion tree, we obtain a sequence of recursive invocations on the arguments
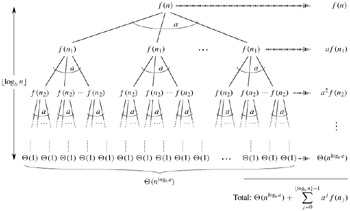
n , ⌈n/b⌉ , ⌈⌈n/b⌉/b⌉ , ⌈⌈⌈n/b⌉/b⌉/b⌉ , ⋮
Let us denote the jth element in the sequence by nj, where
Our first goal is to determine the depth k such that nk is a constant. Using the inequality ⌈x⌉ ≤ x + 1, we obtain
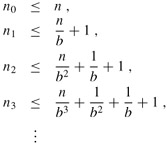
In general,
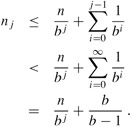
Letting j = ⌊logb n⌋, we obtain
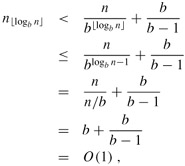
and thus we see that at depth ⌊logb n⌋, the problem size is at most a constant.
From Figure 4.4, we see that
which is much the same as equation (4.6), except that n is an arbitrary integer and not restricted to be an exact power of b.
We can now evaluate the summation
from (4.13) in a manner analogous to the proof of Lemma 4.3. Beginning with case 3, if af(⌈n/b⌉) ≤ cf(n) for n > b + b/(b - 1), where c < 1 is a constant, then it follows that ajf(nj) ≤ cjf(n). Therefore, the sum in equation (4.14) can be evaluated just as in Lemma 4.3. For case 2, we have ![]() . If we can show that
. If we can show that ![]() , then the proof for case 2 of Lemma 4.3 will go through. Observe that j = ≤ ⌊logb n⌋ implies bj/n ≤ 1. The bound
, then the proof for case 2 of Lemma 4.3 will go through. Observe that j = ≤ ⌊logb n⌋ implies bj/n ≤ 1. The bound ![]() implies that there exists a constant c > 0 such that for all sufficiently large nj,
implies that there exists a constant c > 0 such that for all sufficiently large nj,

since ![]() is a constant. Thus, case 2 is proved. The proof of case 1 is almost identical. The key is to prove the bound
is a constant. Thus, case 2 is proved. The proof of case 1 is almost identical. The key is to prove the bound ![]() , which is similar to the corresponding proof of case 2, though the algebra is more intricate.
, which is similar to the corresponding proof of case 2, though the algebra is more intricate.
We have now proved the upper bounds in the master theorem for all integers n. The proof of the lower bounds is similar.
Give a simple and exact expression for nj in equation (4.12) for the case in which b is a positive integer instead of an arbitrary real number.
Show that if ![]() , where k ≥ 0, then the master recurrence has solution
, where k ≥ 0, then the master recurrence has solution ![]() . For simplicity, confine your analysis to exact powers of b.
. For simplicity, confine your analysis to exact powers of b.
Show that case 3 of the master theorem is overstated, in the sense that the regularity condition af(n/b) ≤ cf(n) for some constant c < 1 implies that there exists a constant ∈ > 0 such that ![]() .
.
Give asymptotic upper and lower bounds for T(n) in each of the following recurrences. Assume that T(n) is constant for n ≤ 2. Make your bounds as tight as possible, and justify your answers.
T(n) = 2T(n/2) + n3.
T(n) = T(9n/10) + n.
T(n) = 16T(n/4) + n2.
T (n) = 7T(n/3) + n2.
T(n) = 7T(n/2) + n2.
![]() .
.
T(n) = T(n - 1) + n.
![]() .
.
An array A[1 ‥ n] contains all the integers from 0 to n except one. It would be easy to determine the missing integer in O(n) time by using an auxiliary array B[0 ‥ n] to record which numbers appear in A. In this problem, however, we cannot access an entire integer in A with a single operation. The elements of A are represented in binary, and the only operation we can use to access them is "fetch the jth bit of A[i]," which takes constant time.
Show that if we use only this operation, we can still determine the missing integer in O(n) time.
Throughout this book, we assume that parameter passing during procedure calls takes constant time, even if an N-element array is being passed. This assumption is valid in most systems because a pointer to the array is passed, not the array itself. This problem examines the implications of three parameter-passing strategies:
An array is passed by pointer. Time = Θ(1).
An array is passed by copying. Time = Θ(N), where N is the size of the array.
An array is passed by copying only the subrange that might be accessed by the called procedure. Time = Θ(q - p + 1) if the subarray A[p ‥ q] is passed.
Consider the recursive binary search algorithm for finding a number in a sorted array (see Exercise 2.3-5). Give recurrences for the worst-case running times of binary search when arrays are passed using each of the three methods above, and give good upper bounds on the solutions of the recurrences. Let N be the size of the original problem and n be the size of a subproblem.
Redo part (a) for the MERGE-SORT algorithm from Section 2.3.1.
Give asymptotic upper and lower bounds for T(n) in each of the following recurrences. Assume that T(n) is constant for sufficiently small n. Make your bounds as tight as possible, and justify your answers.
T(n) = 3T(n/2) + n lg n.
T(n) = 5T(n/5) + n/ lg n.
![]()
T(n) = 3T(n/3 + 5) + n/2.
T(n) = 2T(n/2) + n/ lg n.
T(n) = T(n/2) + T(n/4) + T(n/8) + n.
T(n) = T(n - 1) + 1/n.
T(n) = T(n - 1) + lg n.
T(n) = T(n - 2) + 2 lg n.
![]() .
.
This problem develops properties of the Fibonacci numbers, which are defined by recurrence (3.21). We shall use the technique of generating functions to solve the Fibonacci recurrence. Define the generating function (or formal power series) F as
where Fi is the ith Fibonacci number.
Show that F (z) = z + z F (z) + z2F(z).
Show that
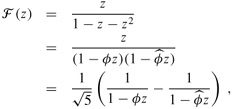
where
and
Show that
Prove that ![]() for i > 0, rounded to the nearest integer. (Hint: Observe
for i > 0, rounded to the nearest integer. (Hint: Observe ![]() .)
.)
Prove that Fi+2 ≥ φi for i ≥ 0.
Professor Diogenes has n supposedly identical VLSI[1] chips that in principle are capable of testing each other. The professor's test jig accommodates two chips at a time. When the jig is loaded, each chip tests the other and reports whether it is good or bad. A good chip always reports accurately whether the other chip is good or bad, but the answer of a bad chip cannot be trusted. Thus, the four possible outcomes of a test are as follows:
|
Chip A says |
Chip B says |
Conclusion |
|---|---|---|
|
|
||
|
B is good |
A is good |
both are good, or both are bad |
|
B is good |
A is bad |
at least one is bad |
|
B is bad |
A is good |
at least one is bad |
|
B is bad |
A is bad |
at least one is bad |
Show that if more than n/2 chips are bad, the professor cannot necessarily determine which chips are good using any strategy based on this kind of pairwise test. Assume that the bad chips can conspire to fool the professor.
Consider the problem of finding a single good chip from among n chips, assuming that more than n/2 of the chips are good. Show that ⌊n/2⌋ pairwise tests are sufficient to reduce the problem to one of nearly half the size.
Show that the good chips can be identified with Θ(n) pairwise tests, assuming that more than n/2 of the chips are good. Give and solve the recurrence that describes the number of tests.
An m × n array A of real numbers is a Monge array if for all i, j, k, and l such that 1 ≤ i < k ≤ m and 1 ≤ j < l ≤ n, we have
A[i, j] + A[k, l] ≤ A[i, l] + A[k, j].
In other words, whenever we pick two rows and two columns of a Monge array and consider the four elements at the intersections of the rows and the columns, the sum of the upper-left and lower-right elements is less or equal to the sum of the lower-left and upper-right elements. For example, the following array is Monge:
|
10 |
17 |
13 |
28 |
23 |
|
17 |
22 |
16 |
29 |
23 |
|
24 |
28 |
22 |
34 |
24 |
|
11 |
13 |
6 |
17 |
7 |
|
45 |
44 |
32 |
37 |
23 |
|
36 |
33 |
19 |
21 |
6 |
|
75 |
66 |
51 |
53 |
34 |
Prove that an array is Monge if and only if for all i = 1, 2, …, m - 1 and j = 1, 2,…, n - 1, we have
A[i, j] + A[i + 1, j + 1] ≤ A[i, j + 1] + A[i + 1, j].
| Note |
(For the "only if" part, use induction separately on rows and columns.) |
The following array is not Monge. Change one element in order to make it Monge. (Hint: Use part (a).)
|
37 |
23 |
22 |
32 |
|
21 |
6 |
7 |
10 |
|
53 |
34 |
30 |
31 |
|
32 |
13 |
9 |
6 |
|
43 |
21 |
15 |
8 |
Let f(i) be the index of the column containing the leftmost minimum element of row i. Prove that f(1) ≤ f(2) ≤ ··· ≤ f(m) for any m × n Monge array.
Here is a description of a divide-and-conquer algorithm that computes the left-most minimum element in each row of an m × n Monge array A:
Construct a submatrix A′ of A consisting of the even-numbered rows of A. Recursively determine the leftmost minimum for each row of A′. Then compute the leftmost minimum in the odd-numbered rows of A.
Explain how to compute the leftmost minimum in the odd-numbered rows of A (given that the leftmost minimum of the even-numbered rows is known) in O(m + n) time.
Write the recurrence describing the running time of the algorithm described in part (d). Show that its solution is O(m + n log m).
[1]VLSI stands for "very large scale integration," which is the integrated-circuit chip technology used to fabricate most microprocessors today.
| < Day Day Up > |