| < Day Day Up > |
This section reviews some standard mathematical functions and notations and explores the relationships among them. It also illustrates the use of the asymptotic notations.
A function f(n) is monotonically increasing if m ≤ n implies f(m) ≤ f(n). Similarly, it is monotonically decreasing if m ≤ n implies f(m) ≥ f(n). A function f(n) is strictly increasing if m < n implies f(m) < f(n) and strictly decreasing if m < n implies f(m) > f(n).
For any real number x, we denote the greatest integer less than or equal to x by ⌊x⌋ (read "the floor of x") and the least integer greater than or equal to x by ⌈x⌉ (read "the ceiling of x"). For all real x,
| (3.3) |
For any integer n,
⌈n/2⌉ + ⌊n/2⌋ = n,
and for any real number n ≥ 0 and integers a, b > 0,
| (3.4) |
| (3.5) |
| (3.6) |
The floor function f(x) = ⌊x⌋ is monotonically increasing, as is the ceiling function f(x) = ⌈x⌉.
For any integer a and any positive integer n, the value a mod n is the remainder (or residue) of the quotient a/n:
| (3.8) |
Given a well-defined notion of the remainder of one integer when divided by another, it is convenient to provide special notation to indicate equality of remainders. If (a mod n) = (b mod n), we write a ≡ b (mod n) and say that a is equivalent to b, modulo n. In other words, a ≡ b (mod n) if a and b have the same remainder when divided by n. Equivalently, a ≡ b (mod n) if and only if n is a divisor of b - a. We write a ≢ b (mod n) if a is not equivalent to b, modulo n.
Given a nonnegative integer d, a polynomial in n of degree d is a function p(n) of the form
where the constants a0, a1, ..., ad are the coefficients of the polynomial and ad ≠ 0. A polynomial is asymptotically positive if and only if ad > 0. For an asymptotically positive polynomial p(n) of degree d, we have p(n) = Θ(nd). For any real constant a ≥ 0, the function na is monotonically increasing, and for any real constant a ≤ 0, the function na is monotonically decreasing. We say that a function f(n) is polynomially bounded if f(n) = O(nk) for some constant k.
For all real a > 0, m, and n, we have the following identities:
|
a0 |
= |
1, |
|
a1 |
= |
a, |
|
a-1 |
= |
1/a, |
|
(am)n |
= |
amn, |
|
(am)n |
= |
(an)m, |
|
am an |
= |
am+n. |
For all n and a ≥ 1, the function an is monotonically increasing in n. When convenient, we shall assume 00 = 1.
The rates of growth of polynomials and exponentials can be related by the following fact. For all real constants a and b such that a > 1,
from which we can conclude that
nb = o(an).
Thus, any exponential function with a base strictly greater than 1 grows faster than any polynomial function.
Using e to denote 2.71828..., the base of the natural logarithm function, we have for all real x,
| (3.10) |
where "!" denotes the factorial function defined later in this section. For all real x, we have the inequality
where equality holds only when x = 0. When |x| ≤ 1, we have the approximation
| (3.12) |
When x → 0, the approximation of ex by 1 + x is quite good:
ex = 1 + x + Θ(x2).
(In this equation, the asymptotic notation is used to describe the limiting behavior as x → 0 rather than as x → ∞.) We have for all x,
We shall use the following notations:
|
lg n |
= |
log2 n |
(binary logarithm) , |
|
ln n |
= |
loge n |
(natural logarithm) , |
|
lgk n |
= |
(lg n)k |
(exponentiation) , |
|
lg lg n |
= |
lg(lg n) |
(composition) . |
An important notational convention we shall adopt is that logarithm functions will apply only to the next term in the formula, so that lg n + k will mean (lg n) + k and not lg(n + k). If we hold b > 1 constant, then for n > 0, the function logb n is strictly increasing.
For all real a > 0, b > 0, c > 0, and n,
where, in each equation above, logarithm bases are not 1.
By equation (3.14), changing the base of a logarithm from one constant to another only changes the value of the logarithm by a constant factor, and so we shall often use the notation "lg n" when we don't care about constant factors, such as in O-notation. Computer scientists find 2 to be the most natural base for logarithms because so many algorithms and data structures involve splitting a problem into two parts.
There is a simple series expansion for ln(1 + x) when |x| < 1:
We also have the following inequalities for x > -1:
| (3.16) |
where equality holds only for x = 0.
We say that a function f(n) is polylogarithmically bounded if f(n) = O(lgk n) for some constant k. We can relate the growth of polynomials and polylogarithms by substituting lg n for n and 2a for a in equation (3.9), yielding
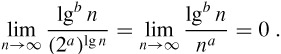
From this limit, we can conclude that
lgb n = o(na)
for any constant a > 0. Thus, any positive polynomial function grows faster than any polylogarithmic function.
The notation n! (read "n factorial") is defined for integers n ≥ 0 as
Thus, n! = 1 · 2 · 3 n.
A weak upper bound on the factorial function is n! ≤ nn, since each of the n terms in the factorial product is at most n. Stirling's approximation,
where e is the base of the natural logarithm, gives us a tighter upper bound, and a lower bound as well. One can prove (see Exercise 3.2-3)
where Stirling's approximation is helpful in proving equation (3.18). The following equation also holds for all n ≥ 1:
where
| (3.20) |
We use the notation f(i)(n) to denote the function f(n) iteratively applied i times to an initial value of n. Formally, let f(n) be a function over the reals. For nonnegative integers i, we recursively define
For example, if f(n) = 2n, then f(i)(n) = 2in.
We use the notation lg* n (read "log star of n") to denote the iterated logarithm, which is defined as follows. Let lg(i) n be as defined above, with f(n) = lg n. Because the logarithm of a nonpositive number is undefined, lg(i) n is defined only if lg(i-1) n > 0. Be sure to distinguish lg(i) n (the logarithm function applied i times in succession, starting with argument n) from lgi n (the logarithm of n raised to the ith power). The iterated logarithm function is defined as
lg* n = min {i = 0: lg(i) n ≤ 1}.
The iterated logarithm is a very slowly growing function:
|
lg* 2 |
= |
1, |
|
lg* 4 |
= |
2, |
|
lg* 16 |
= |
3, |
|
lg* 65536 |
= |
4, |
|
lg*(265536) |
= |
5. |
Since the number of atoms in the observable universe is estimated to be about 1080, which is much less than 265536, we rarely encounter an input size n such that lg* n > 5.
The Fibonacci numbers are defined by the following recurrence:
Thus, each Fibonacci number is the sum of the two previous ones, yielding the sequence
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ... .
Fibonacci numbers are related to the golden ratio φ and to its conjugate ![]() , which are given by the following formulas:
, which are given by the following formulas:
Specifically, we have
| (3.23) |
which can be proved by induction (Exercise 3.2-6). Since ![]() , we have
, we have ![]() , so that the ith Fibonacci number Fi is equal to
, so that the ith Fibonacci number Fi is equal to ![]() rounded to the nearest integer. Thus, Fibonacci numbers grow exponentially.
rounded to the nearest integer. Thus, Fibonacci numbers grow exponentially.
Show that if f(n) and g(n) are monotonically increasing functions, then so are the functions f(n) + g(n) and f (g(n)), and if f(n) and g(n) are in addition nonnegative, then f(n) · g(n) is monotonically increasing.
Is the function ⌈lg n⌉! polynomially bounded? Is the function ⌈lg lg n⌉! polynomially bounded?
Prove by induction that the ith Fibonacci number satisfies the equality
where φ is the golden ratio and ![]() is its conjugate.
is its conjugate.
Let
where ad > 0, be a degree-d polynomial in n, and let k be a constant. Use the definitions of the asymptotic notations to prove the following properties.
If k ≥ d, then p(n) = O(nk).
If k ≤ d, then p(n) = Ω(nk).
If k = d, then p(n) = Θ(nk).
If k > d, then p(n) = o(nk).
If k < d, then p(n) = ω(nk).
Indicate, for each pair of expressions (A, B) in the table below, whether A is O, o, Ω, ω, or Θ of B. Assume that k ≥ 1, ∈ > 0, and c > 1 are constants. Your answer should be in the form of the table with "yes" or "no" written in each box.
|
A |
B |
O |
o |
Ω |
ω |
Θ |
|
|---|---|---|---|---|---|---|---|
|
a. |
lgk n |
n∈ | |||||
|
b. |
nk |
cn | |||||
|
c. |
|
nsin n | |||||
|
d. |
2n |
2n/2 | |||||
|
e. |
nlg c |
clg n | |||||
|
f. |
lg(n!) |
lg(nn) |
Rank the following functions by order of growth; that is, find an arrangement g1, g2, ..., g30 of the functions satisfying g1 = Ω(g2), g2 = Ω(g3), ..., g29 = Ω(g30). Partition your list into equivalence classes such that f(n) and g(n) are in the same class if and only if f(n) = Θ(g(n)).
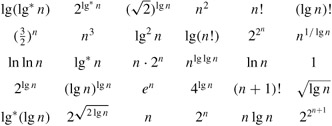
Give an example of a single nonnegative function f(n) such that for all functions gi(n) in part (a), f(n) is neither O(gi(n)) nor Ω(gi(n)).
Let f(n) and g(n) be asymptotically positive functions. Prove or disprove each of the following conjectures.
f(n) = O(g(n)) implies g(n) = O(f(n)).
f(n) + g(n) = Θ(min(f(n), g(n))).
f(n) = O(g(n)) implies lg(f(n)) = O(lg(g(n))), where lg(g(n)) ≥ 1 and f(n) ≥ 1 for all sufficiently large n.
f(n) = O(g(n)) implies 2f(n) = O (2g(n)).
f(n) = O((f(n))2).
f(n) = O(g(n)) implies g(n) = Ω(f(n)).
f(n) = Θ(f(n/2)).
f(n) + o( f(n)) = Θ(f(n)).
Some authors define Ω in a slightly different way than we do; let's use ![]() (read "omega infinity") for this alternative definition. We say that
(read "omega infinity") for this alternative definition. We say that ![]() if there exists a positive constant c such that f(n) ≥ cg(n) ≥ 0 for infinitely many integers n.
if there exists a positive constant c such that f(n) ≥ cg(n) ≥ 0 for infinitely many integers n.
Show that for any two functions f(n) and g(n) that are asymptotically nonnegative, either f(n) = O(g(n)) or ![]() or both, whereas this is not true if we use Ω in place of
or both, whereas this is not true if we use Ω in place of ![]() .
.
Describe the potential advantages and disadvantages of using ![]() instead of Ω to characterize the running times of programs.
instead of Ω to characterize the running times of programs.
Some authors also define O in a slightly different manner; let's use O' for the alternative definition. We say that f(n) = O'(g(n)) if and only if |f(n)| = O(g(n)).
What happens to each direction of the "if and only if" in Theorem 3.1 if we substitute O' for O but still use Ω?
Some authors define Õ (read "soft-oh") to mean O with logarithmic factors ignored:
Õ (g(n)) = {f(n): there exist positive constants c, k, and n0 such that 0 ≤ f(n) ≤ cg(n) lgk(n) for all n ≥ n0}.
Define ![]() and
and ![]() in a similar manner. Prove the corresponding analog to Theorem 3.1.
in a similar manner. Prove the corresponding analog to Theorem 3.1.
The iteration operator* used in the lg* function can be applied to any monotonically increasing function f(n) over the reals. For a given constant c ∈ R, we define the iterated function ![]() by
by
which need not be well-defined in all cases. In other words, the quantity ![]() is the number of iterated applications of the function f required to reduce its argument down to c or less.
is the number of iterated applications of the function f required to reduce its argument down to c or less.
For each of the following functions f(n) and constants c, give as tight a bound as possible on ![]() .
.
|
f(n) |
c |
|
|
|---|---|---|---|
|
a. |
n - 1 |
0 | |
|
b. |
lg n |
1 | |
|
c. |
n/2 |
1 | |
|
d. |
n/2 |
2 | |
|
e. |
|
2 | |
|
f. |
|
1 | |
|
g. |
n1/3 |
2 | |
|
h. |
n/lg n |
2 |
| < Day Day Up > |